Algorithm Analysis: NP problems 2
알고리즘 관련 모든 글은 연세대학교 안형찬 교수님의 CSI_3108: Algorithm Analysis의 강의 내용과 자료입니다.
지난 시간에 이어서 이번에는 Polynomial-time reduction을 실제로 해보도록 하겠습니다. 가장 기초적인 문제로 우선 Independent set을 보겠습니다. Independent 하다는 게 뭔지부터 정의하겠습니다.
Definition 1. Given a graph $G = (V, E)$, we say $S \subseteq V$ is independent if no two nodes in $S$ are adjacent.
그래프에서 두 노드가 서로 edge 하나로 이어져있지 않다면 그 두 노드는 서로 independent 합니다.
Independent set problem
Problem 1. Given a graph $G = (V, E)$ and an integer $k$, does $G$ have an independent set of size at least $k$?
결과적으로 서로 인접해있지 않게 node들을 고르는 문제입니다. Node 개수가 작은 independent set은 찾기 쉽습니다. 극단적으로, 1개의 node만 고르면 무조건 independent set이 됩니다. 그러나 node 개수가 많은 independent set 찾기는 어렵습니다. 그렇기 때문에 independent set problem에서는 최소 몇 개의 node는 갖는 independent set이 존재하는지 여부가 문제입니다(decision problem). “최소” 개념이 잘 와닿지 않을 수 있습니다. 쉽게 이야기해서, “Independent set 찾을 때 이 정도 node 개수는 써야지, 작은 개수 찾기는 쉽잖아?” 정도 되겠습니다.
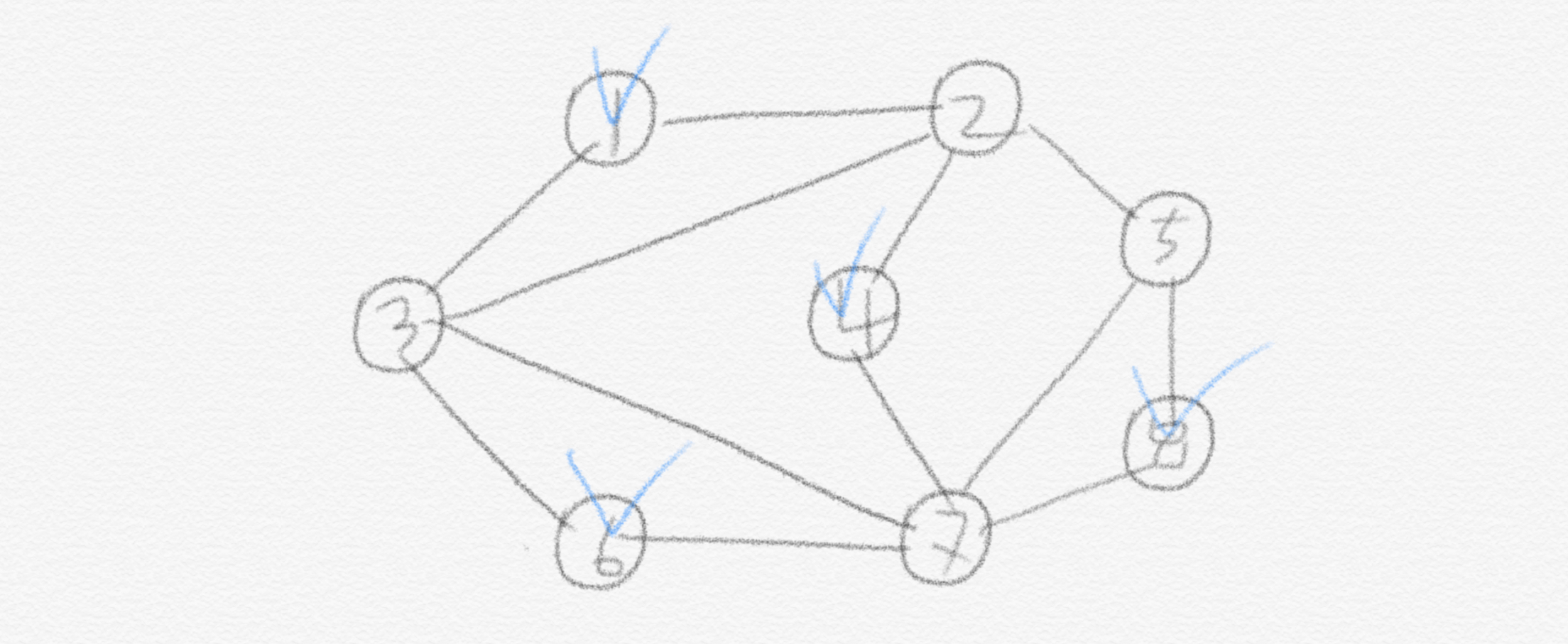
Remark 1. We can define an optimization version of this problem as follows: given a graph $G = (V, E)$, determine the maximum cardinality of an independent set. In fact, these two versions of the problem are “equally hard”: if we can solve the optimization version, it is easy to solve the decision version. If we can solve the decision version, then by repeatedly solving the decision version for $k = 0, . . . , |V|$, we can solve the optimization version as well. (This can be made slightly faster by using binary search.) This equivalence shows why our previous assumption that all problems have only yes/no answers was reasonable. In fact, for any problem with a “long” output, we could just define a decision problem that, given $i$, asks whether the $i-th$ bit of the long output is 1 or not. It is clear that those two problems are equally hard.
앞서 이전 글에서 말했듯이 optimization 버전의 문제와 decision 버전의 문제는 사실 별반 차이가 없습니다. 위에서 하나 참고로 언급하는 것은 binary search로 좀더 빨리 optimization 버전을 풀 수 있다는 사실입니다. 이전 글에서의 내용을 다시 보겠습니다.
반대로 우리가 해당 decision problem 버전을 다 풀어서 주어진 interval scheduling 문제에서는 7개를 기준으로 답이 yes와 no로 갈린다고 하면, optimization 버전의 답은 7이 되는 셈입니다.
이때 여기서 이 7이라는 숫자를 찾는 방법으로 binary search를 쓰겠다는 의미입니다. 수많은 숫자 중에서 어느 하나를 잡고, 예를 들어 11, 이에 대한 decision problem을 풉니다. “최소 11개를 소화할 수 있는 interval schedule이 존재하는가?”. 만약 이 문제의 답이 no 면 당연히 11보다 작은 숫자로 시도해보아야 합니다. 절반을 줄인 5로 해보니까 답이 yes라 나옵니다. 그러면 이제 5와 11 사이 중간 숫자로 시도해봅니다. 이렇게 binary search 식으로 decision problem들을 풀어보면 모든 숫자에 대해 decision problem을 풀지 않아도 됩니다.
Vertex cover problem
이제 다음으로 또다른 문제를 소개하겠습니다.
Definition 1. Given a graph $G = (V, E)$, we say $S \subseteq V$ is a vertex cover if every edge $e \in E$ has at least one of its two endpoints contained in $S$.
만약에 node들로 이루어진 부분집합 $S$ 에서 그 원소인 node들에 인접한 edge들의 집합이 graph $G$의 전체 edge와 같으면 이 부분집합 $S$ 는 vertex cover입니다. 쉽게 말해 $S$ 에 있는 node들이 전체 edge 집합 $E$ 를 커버하면 $S$는 vertex cover 입니다.
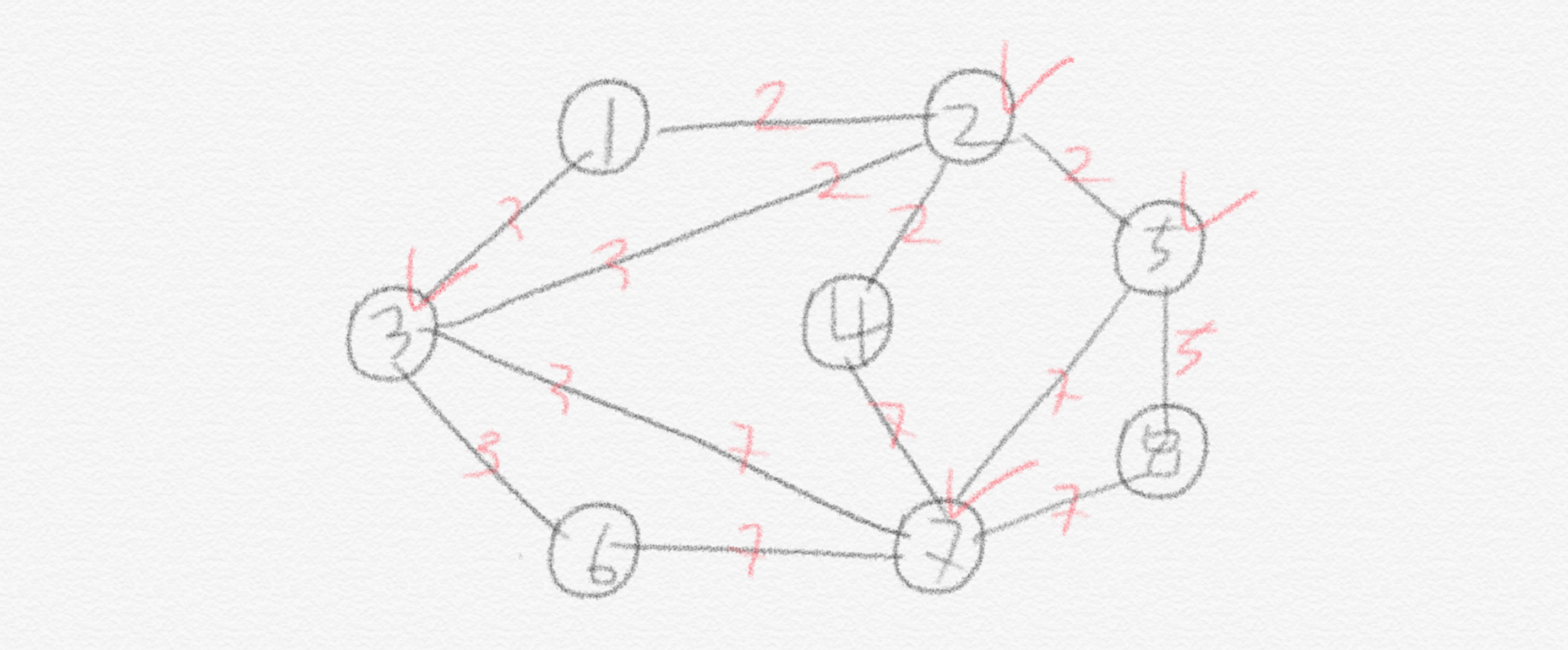
Problem 2 (Vertex Cover). Given a graph $G = (V, E)$ and an integer $k$, does $G$ have a vertex cover of size at most $k$?
Node들로 전체 edge를 커버할 수 있는지 여부를 묻는 문제이기 때문에 당연히 $S$의 node 개수가 많으면 그만큼 인접한 edge도 많아지니 vertex cover를 만들기는 쉽습니다. 적은 수의 node들만으로 전체 edge를 커버하기가 까다롭습니다. 따라서 여기서는 최대 몇 개의 node(또는 vertex)를 $S$에 포함시킬지 제약을 겁니다. Independent set에서는 최소 $k$ 개의 vertex는 써야 한다고 한 것과는 반대입니다. 이 “최대” 개념은 쉽게 이야기해서, “최대 이 정도 vertex 개수는 써도 괜찮으니까, vertex cover를 찾아봐” 정도 되겠습니다.
Polynomial-time reduction in both ways
비록 아직까지 independent set이나 vertex cover 문제를 polynomial-time에 푸는 효율적인 알고리즘은 밝혀지지 않았습니다. 하지만 우리는 두 문제의 상대적 난이도는 판가름할 수 있습니다. 이제부터 이 두 문제가 동등한 난이도를 갖고 있다는 사실을 증명하겠습니다. 어떤 두 문제의 상대적 “난이도”를 보일 때는 polynomial-time reduction을 이용합니다. $Y \le_p X$ 일 때, $X$ 가 더 쉽지 않은 문제라는 사실을 알 수 있었습니다. 따라서 두 문제가 동등한 난이도를 갖는다는 사실을 보이려면, $Y \le_p X$ 와 $X \le_p Y$ 양방향을 보이면 됩니다.
따라서 $IndependentSet \le_p VertexCover$ 와 $VertexCover \le_p IndependentSet$ 양방향의 polynomial-time reduction을 보이면 아래와 같은 사실을 증명할 수 있습니다.
Lemma 1. Let $G = (V, E)$ be a graph. Then $S \subseteq V$ is an independent set if and only if $V$ \ $S$ 1 is a vertex cover.
$Proof.$
우선 두 문제가 구조적으로 같은 문제라는 사실부터 보이겠습니다.
처음으로 $S$ 가 Independent Set 일 때 $V$ \ $S$ 는 vertex cover 가 된다는 방향부터 증명하겠습니다. $S \subseteq V$ 가 independent set 이라면, $S$ 에 있는 vertex들은 서로 인접하지 않습니다. 그러므로 $S$ 의 어떠한 두 vertex 도 edge를 서로 사이에 두고 있지 않습니다. 만약에 $S$ 의 두 vertex 가 어떤 하나의 edge로 연결되어 있다면, 이미 두 vertex가 인접한 거니까 그 $S$ 는 independent set일 수 없습니다. 이를 좀더 엄밀히 이야기하면 graph $G$의 어떠한 edge도 양끝에 “$S$ 에 속한 두 vertex”를 두고 있지 않다는 의미가 됩니다. 또 다르게 표현하면 어떠한 edge $(u,v)$2 에서 적어도 한 vertex는 $S$ 에 속하지 않는 것입니다, $u \notin S$ or $v \notin S$ (or both not in $S$). 바꿔 이야기하면 edge $(u,v)$ 에서 양끝 vertex 중 적어도 하나는 $V$ \ $S$ 에 속하게 됩니다. 따라서 모든 edge를 vertex로 다 커버해야 한다는 Vertex cover 정의에 따라 $V$ \ $S$ 는 Vertex cover입니다.
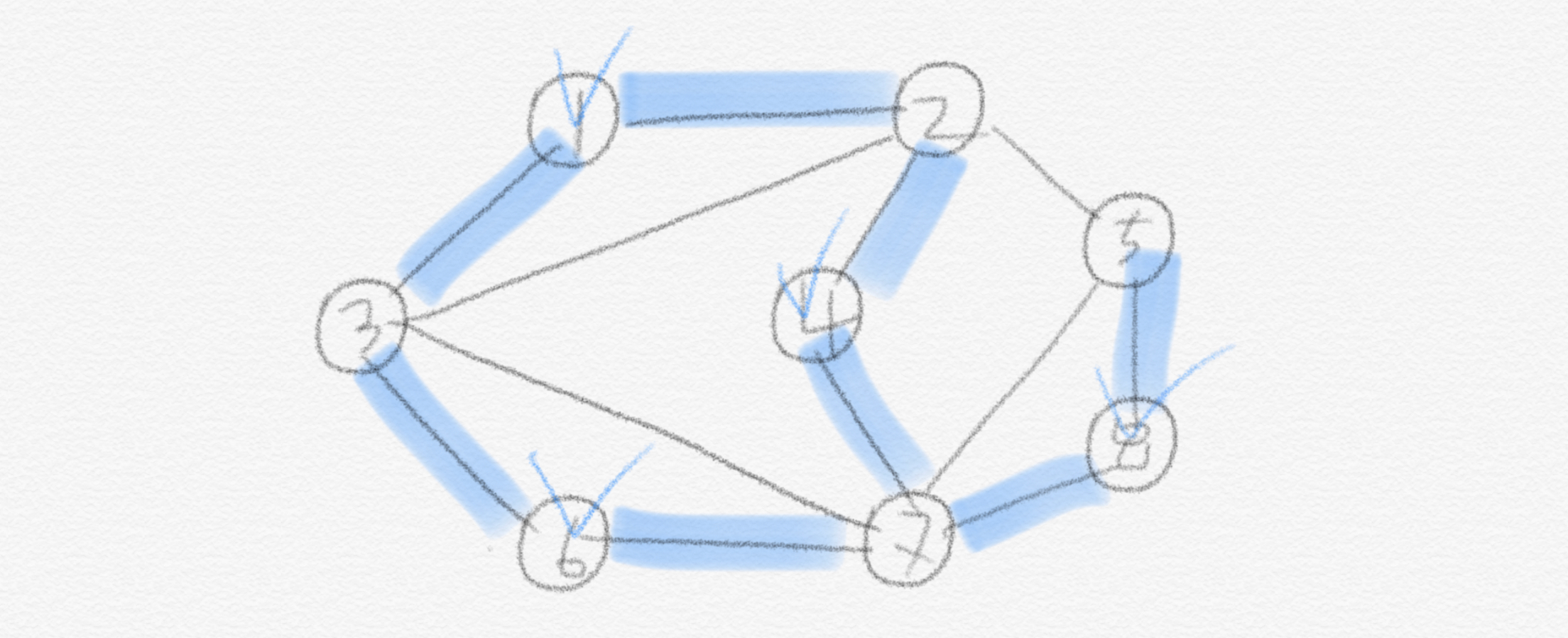
이제는 반대 방향을 증명하겠습니다.
$V$ \ $S$ 가 vertex cover 라 가정하겠습니다. 그리고 $u$ 와 $v$ 는 $S$ 에 있는 임의의 두 vertex라고 하겠습니다. 그렇다면 당연히 $S$ 에 있는 이 두 vertex들은 $V$ \ $S$ 에는 없을 것입니다. 이 두 vertex가 $V$ \ $S$ 에 없다는 것은 그 두 vertex 사이를 연결하는 edge $(u,v)$ 가 graph $G$ 상에 존재하지 않는 edge라는 의미가 됩니다. 왜냐하면 $V$ \ $S$ 가 vertex cover이기 때문에 graph $G$ 에 있는 모든 edge를 다 커버하기 때문입니다. 모든 edge 를 커버하는 게 vertex cover인데 그 vertex cover에 의해 커버되지 않는 edge라면 그것은 $G$ 에 존재할 수 없는 edge 인 것입니다. 따라서 $u$, $v$ 사이를 잇는 edge는 존재하지 않으므로 두 vertex는 인접하지 않습니다. 따라서 $S$ 에 있는 모든 vertex 들은 서로 인접하지 않습니다. 그러므로 $V$ \ $S$ 가 vertex cover 일 때 $S$ 는 independent set 이 됩니다.
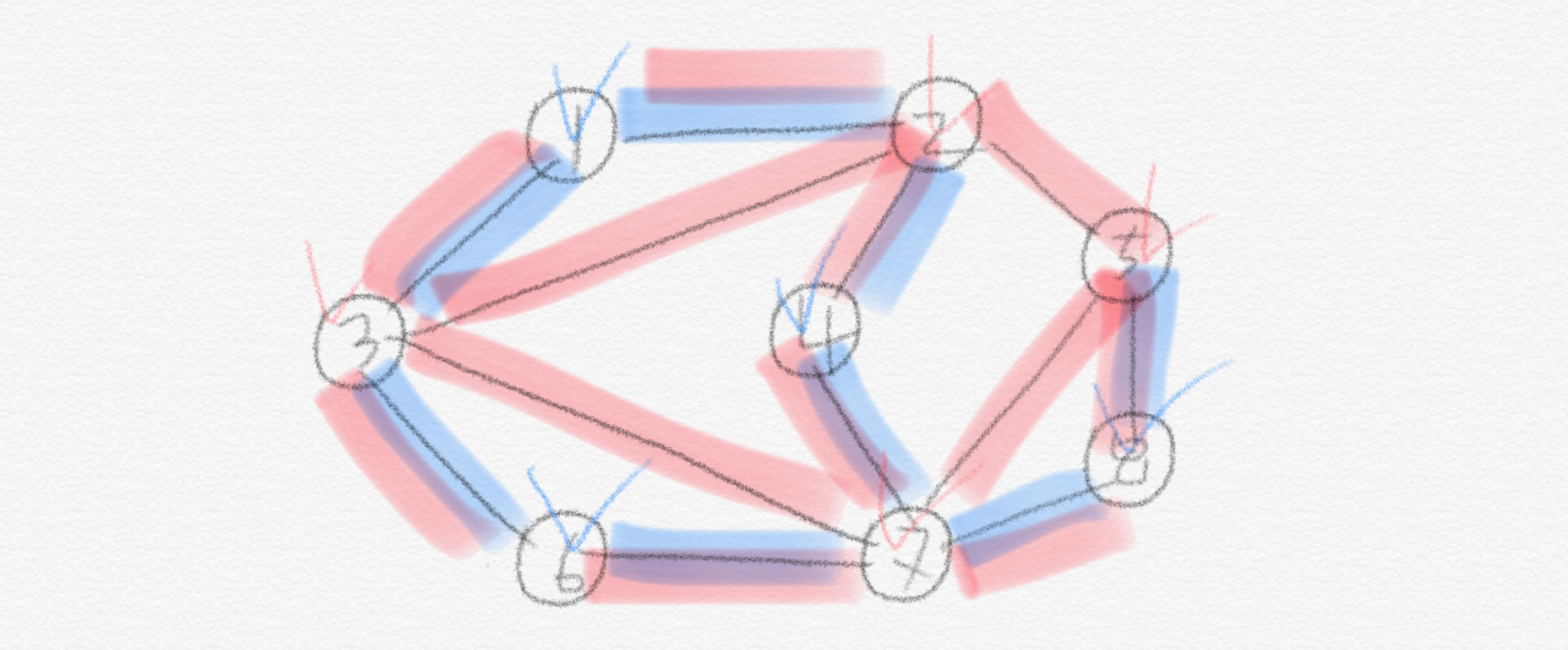
이렇게 Independent set과 Vertex cover는 굉장히 밀접하게 연관이 있는 문제입니다. 이제 이 두 문제의 상대적 난이도를 보이기 위해 polynomial-time reduction을 시켜보겠습니다. Polynomial-time reduction 에서 주의해야 할 점 중 하나는, 그 방향입니다. 어느 문제에서 어느 문제로 reduction을 시켜야 하는지를 학생들이 많이 헷갈려 합니다. 그리고 실제로 시험에서도 많이 실수한다고 합니다.
다시 한 번 되짚어 보면, 어떤 문제 $A$ 가 다른 문제 $B$ 보다 쉽지 않다는 사실을 보이기 위해서는 그 다른 문제 $B$ 에서 $A$ 로 reduction 시켜야 합니다!
지금 우리는 우선 Vertex Cover가 Independent set보다 쉽지 않은 문제임을 보이기 위해 아래와 같이 reduction 시키겠습니다.
Theorem 1. Independent Set $\le_p$ Vertex Cover.
$Proof.$
Vertex Cover 를 푸는 블랙박스가 주어져있다고 할 때, 이를 이용해서 Independent Set 은 쉽게 풀 수 있습니다. Vertex cover를 푸는 블랙박스에 필요한 input은 graph $G=(V,E)$ 와 최대 몇 개의 vertex를 사용해도 되는지에 대한 제약입니다. 이는 우리의 Independent set 으로부터 쉽게 만들어낼 수 있다. Graph $G$ 는 그냥 그대로 넣으면 됩니다. 그리고 Independent set 문제에 주어지는 최소 몇 개의 vertex는 사용해야 되는지에 대한 제약이었던 $k$ 를 이용해서 Vertex cover 문제의 최대 vertex 개수 제약을 표현해야 합니다. 앞서서 Independent set $S$ 가 주어졌을 때, $V$ \ $S$ (전체 Vertex set에서 $S$ 만 뺀 부분집합)가 Vertex cover 였다는 사실을 이용하면 vertex 최대 개수 제약조건은 $|V|-k$ 임을 알 수 있습니다. 최소 $k$ 개 는 쓰는 Independent set $S$ 는 곧, 최대 $|V|-k$ 개의 vertex를 쓰는 Vertex cover 와 대응됩니다. 이렇게 Vertex cover 를 위한 블랙박스에 넘겨주면 그 가상의 블랙박스는 바로 답을 내어줄 것입니다. 결과가 yes면 Independent set도 yes instance 입니다. 여기서는 딱히 문제 형태의 변환이 필요 없으므로 당연히 polynomial time 에 변형이 가능합니다. 그리고 Lemma 1. 에서 봤듯이 두 문제는 사실상 같은 문제라고 볼 수 있으므로 한 문제가 yes instance 일 때 다른 문제도 yes instance 인지를 따로 보일 필요는 없습니다. 그러므로 이는 Polynomial-time reduction 이 가능함을 알 수 있습니다.
Theorem 2. Vertex Cover $\le_p$ Independent Set.
위의 과정과 대칭이므로 증명은 생략하겠습니다.
Theorem 1과 2에 의해서 양방향 polynomial-time reduction이 가능함을 보였습니다. 따라서 두 문제의 상대적 난이도는 같음을 알 수 있습니다.
정리
Polynomial-time reduction 과정을 정리해보겠습니다. 가장 헷갈리는 것은 방향입니다. 다른 문제 $Y$ 를 이용해서 더 쉽지는 않다(not easier, at least as hard as)고 보이고 싶은 문제 $X$ 의 형태로 변형시키는 과정입니다. 따라서 이 부등호 $\le_p$ 오른편에 오는 문제가 더 쉽지는 않은 문제가 되는 것입니다. 이를 위해서는 3가지를 보여야 합니다.
- 부등호 왼편의 문제를 부등호 오른편에 오는 문제의 형태로 polynomial time 안에 바꿀 수 있어야 합니다
- 부등호 왼편 문제가 yes instance 일 때, 오른편 문제의 형태도 yes instance 여야 합니다.
- 부등호 왼편 문제가 no instance 일 때, 오른편 문제의 형태도 no instance 여야 합니다.
- (오른편 문제의 형태로 바뀐 것이 yes instance 일 때, 왼편 문제도 yes instance 여야 합니다.) 와 같은 말입니다.
다음 글에서는 Vertex cover보다 좀더 일반적인 형태의 문제를 살펴보고, 이로 polynomial-time reduction을 시켜보겠습니다.
- Algorithm Analysis - NP Problems 1 SERIES 1/5
- Algorithm Analysis - NP Problems 2 ✓ SERIES 2/5
- Algorithm Analysis - NP Problems 3 SERIES 3/5
- Algorithm Analysis - NP Problems 4 SERIES 4/5
- Algorithm Analysis - NP Problems 5 SERIES 5/5